Apsidendrehung (und eigentlich sogar Himmelsmechanik-Basics) – Teil 1 von 2

Ich kannte es bisher eher als Periheldrehung, aber Apsidendrehung als allgemeinen Begriff zu verwenden, erscheint mir sinnvoll. Ähm. Noch was anderes: Ich habe ja geschrieben, dass ich mehr Zeit hätte, ja, es stimmt, aber ist auch tagesäbhangig, es gibt auch Tage, an denen ich echt ziemlich viel tun muss. Ich sitze aber im Moment noch an einem anderen Dokument, welches zwar in Zeit liegt und für u.a. GSA gedacht ist (Die Geheimnisse von Maugri) und daher kommen jetzt auch nicht öfters Beiträge. Ich versuche mir immer neue Themen einfallen zu lassen, (aktuell gibt es viel Input!), und an der Astronomie-Geschichte weiterzuschreiben, aber es gibt weiterhin vermutlich im 3-Tage-Zyklus halbregelmäßig Beiträge. So! Genug dazu.

Wir kennen ja alle unser Sonnensystem, ja? Da gibt es acht Planeten, Merkur bis Neptun, da gibt es auch unzählige verschiedene Himmelskörper, die sonst noch im Sonnensystem verweilen und glücklich ihre Bahnen ziehen.
Genau, sie ziehen Bahnen. Das ist schon eine ganz alte Erkenntnis, die wir schon seit mindestens 5 Tausend Jahren oder mehr haben. Man brauchte den Himmel über wenige Jahre sich ansehen und bereits wichtige andere Erkenntnisse machen. Z.B. gibt es dort den Mond, eine kugelrunde Fläche welche abhängig von der Sonne angestrahlt wird und dementsprechend dann einen Stand am Himmel hat. Man hat auch 5 weitere „Wandelgestirne“ bemerkt, welche über Wochen sich relativ zu den Fixsternen bewegen, da gab es schnelle Wandelgestirne und langsamere, es gab die Venus und den Merkur, die scheinbar eine andere Art von Bahn besitzen und immer der Sonne nahe bleiben und die Helligkeit auch verändern und die anderen drei Wandelgestirne, welche eine Bahn beschreiben, die der (scheinbaren) Sonnenbahn, auch Ekliptik, ähneln. Doch wenn man sie genau beobachtet, und auch die, die immer nahe an der Sonne liegen, haben nach einer gewissen Zeit eine höchst eigenartige Flugbahn: Sie fliegen in einem bestimmten Zeitrahmen plötzlich eine Schleife. Ja, sie wandern für meist einige Wochen rückläufig, erreichen den Stillstand, und bewegen sich wieder normal. Das macht der Jupiter alle 13 Monate, der Saturn etwa alle 12 ½ Monate und der Mars nur alle 26 Monate. Bei der ersten Kategorie erreicht die Venus den Ausgangspunkt nach etwa 7 ½ wieder und der Merkur sogar nach fast 4 Monaten wieder. Wobei ich sagen muss, dass es auch damals ohne Lichtverschmutzung es schwierig geworden wäre, den Merkur zu sichten.

Die Menschen taten sich immer besser darin, die Planetenbahnen genau vorherzusagen. Sie konnten sich schon vor der Antike zusammenreimen, dass diese Schleifen, und Häufigkeit der Schleifen, Helligkeit und die Geschwindigkeit, den Fixsternhimmel einmal zu umrunden, scheinbar eine Reihenfolge vorgibt. Man stellte sich oft die Sonne als Zentrum vor und alle anderen Wandelgestirne inklusive der Erde als Trabanten. Der Mond kreiste ohne eine Veränderung der Oberflächenform weiterhin um die Erde und man stellte sich ihn daher als Erdtrabant vor. Es ist das Heliozentrische Weltbild, mehr oder minder. Neben dem gab es auch noch das geozentrische Weltbild. Die Erde ist der Mittelpunkt der Welt und alle Planeten (Die Sonne und der Mond sind für das damalige Verständnis so etwas ähnliches) drehen sich um die Erde. Um die Schleifenbahnen der Planeten zu erklären, bewegen sich die Planeten noch zusätzlich auf „Nebenkreisen“ (welche natürlich befestigt sein müssen, ist ja klar…; das ist übrigens die Epizykeltheorie) und so um die Erde. Allerdings ist dieses Modell viel mehr komplexer, als das erste Weltbild und es sollt sich auch als das richtige herausstellen, auch wenn noch Feinarbeit an dem Heliozentrischen Weltbild notwendig war. Dann kam Kepler mit seinen Rudolfinischen Tafeln in der frühen Neuzeit und brachte die Erkenntnis. Die Bahnen der Planeten konnten nun jahrelang vorausbestimmt werden ohne größere Abweichungen. Aber Kepler brachte nicht die Erkenntnis, warum sie sich bewegen. Warum bewegten sie sich immer noch in angenäherte Kreisbahnen, bzw. Kegelausschnitte/Ellipsen? Das konnte man mit dem Wissen von Kepler nicht herausfinden. Kepler benutzte für seine drei Keplerschen Gesetze die Daten der Marsbahn, welche für die Präteleskopische Ära äußerst akkurat waren. Der Fehler lag nur bei vielleicht einer Bogenminute! Wir kennen alle die Formeln des Keplers?

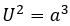
Das bedeutet, dass

und

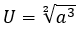
ist. Die Variablen folgern hier interessanterweise AE und Jahr, daraus kann man ein Verhältnis erhalten:

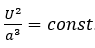
Dann kam Newton. Er revolutionierte die Astronomie mit seiner Entdeckung der Mechanik hinter den Planetenbewegungen: Die Gravitation! Alles was Masse besitzt, vom Neutrino bis zum Großen Attraktor zeiht alle sonstige Materie des Universums an. Zum Glück ist die Gravitation gar nicht so stark, oder? Stell dir mal vor, wie es wäre, wenn alles in deiner Nähe zu deinem Körper hingezogen wird, oder Seifenblasen sich gegenseitig anziehen würden, oder gar die Luft sich verklumpen würde! Zwar wären wir dann von der Übermasse unter uns (dein Heimatplanet) zu einem Teilchenbrei zusammengequetscht. Okay, genug davon. Die Gravitation ist nämlich die schwächste, der vier bekannten Grundkräfte. Es gibt zwei verschiedene Gravitationskonstanten, wobei jedoch die eine mit veralteten Einheiten, bzw. mit non-SI-Einheiten arbeitet. Logischerweise haben jedoch beide Zahlen denselben Wert. Einmal die SI-Gravitationskonstante mit

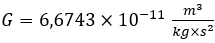
Und das zweite die sog. „Gaußsche Gravitationskonstante, wobei … ich sag sie euch doch nicht, es verwirrt nur. Ich habe einen Link anbei gesetzt. Dabei ist die Anziehungskraft zwischen zwei kugelsymmetrischen Körpern bei

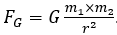
Wenn zwei Bleikugeln mit jeweils einem Radius von 10 cm 40 cm vom Mittelpunkt her gesehen auseinander liegen, (Dichte: 11,342 g/cm², Masse bei RT (Raumteperatur):

) liegt die gemeinsame Anziehungskraft bei

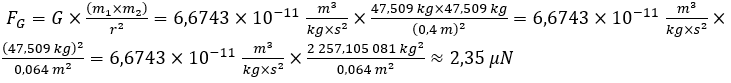
Diese zwei Bleikugeln ziehen sich mit 2,35 µN an. Das ist wenig, sehr wenig. Auf der Erde würden 240,5 ng so eine Gewichtskraft ausüben. Es wäre auch am wenigsten schlimm, wenn sich die universelle Gravitationskonstante im Universum geringfügig verändern würde. Deshalb ist die Gravitation in der Astroteilchenphysik sehr irrelevant. Nicht nur die Anziehungskraft zwischen zwei Objekten konnte ermittelt werden, sondern auch die Masse der Erde, welche wichtig für Bahnberechnungen der Erde sind. G ist die Gravitationskonstante, M_E ist die Erdmasse und r die Entfernung vom Erdmittelpunkt.

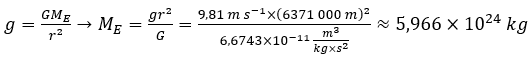
Jetzt wusste man warum die Planeten sich um die Sonne drehen. Sie mussten eine gewaltige Masse haben. Heute kennt man die Sonnenmasse relativ genau und man hat sie auf

bestimmen können. Und man konnte die Geschwindigkeit der Planeten bestimmen. Man konnte jetzt durch die Umlaufszeit von z.B. Merkur mit Berücksichtigung der Eigenbewegung der Erde gut berechnen. In einer Kreisbahn sollten sich die Gravitationskräfte und die Zentripetalkräfte die Waage halten, die sie durch ihre immense Geschwindigkeit erzeugen. Also können wir die beiden Formeln dafür gleichsetzen.

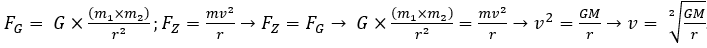
. Das können wir an einem Beispiel Sonne – Erde testen: Die Masse der Sonne steht schon oben. Die Masse der Erde haben wir bereits auch ausgerechnet. Der Abstand der Erde zur Sonne beträgt im Mittel eine AE. Das sind 149 597 870 700 Meter. Hier kommt die Rechnung:

. Mit so genauen Zahlen zu rechnen macht nicht unbedingt so viel Sinn, da es genügend andere Störfaktoren gibt. Die erste Möglichkeit ist nicht unbedingt ein Störfaktor, sondern einfach der Fakt, dass die Erde keine wirkliche Kreisbahn hat und diese Bahngeschwindigkeit nur bei dieser Entfernung tatsächlich hat, denn die Entfernung ist die Große Halbachse (a), die mittlere Entfernung. Um herauszufinden, wie schnell die Erde ist, wenn sie 152 Mio. km von der Sonne weg ist, oder aber auch nur, wenn die Erde gerade mal 147 Mio. km von ihr entfernt ist, brauchen wir die Vis-Viva-Gleichung:

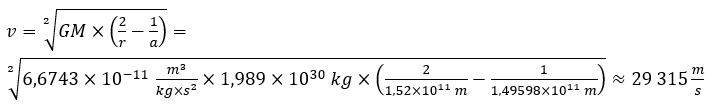
. Die Geschwindigkeit ist also in der Erdferne nur wenig verschieden.

Beim nächsten Teil, welcher bestimmt in etwa einer Woche herauskommt, bist du bestimmt schon Profi darin und dann schauen wir uns die ganz harte Nummer an, die Apsidendrehung. Mein nächster Beitrag handelt sich wieder um Galileo und wird vermutlich ähnlich lang wie dieser Beitrag werden. Im Moment kam nicht so viel wegen dieses längeren Beitrags und wegen dem einen anderen großem Dokument nichts. Ich denke, ich werde mich in dieser Zeit mehr auf kleine Themen konzentrieren, nach dem zweiten Teil hiervon neben meinem großen Dokument und die Geschichte der Astronomie.

Quellen:

• Kompendium der Astronomie, Hans-Ulrich Keller, Kosmos, 2019, ISBN 978-3-440-16276-7, Kapitel 3
• Die Geschichte der Astronomie: von Kopernikus bis Stephen Hawking, Peter Aughton, National Geographic Deutschland, 2009, ISBN: 978-3-866-90113-1