Letztes Mal haben wir uns angesehen, wie so grob die Gravitation für Konsequenzen haben und auch sogar mathematisch. Leider habe ich immer noch kein Plugin, oder HTML-Ding für Formeln gefunden, sonst würde ich sie nicht in ein Bild packen. Heute gehe ich näher auf ein Problem der Himmelsmechanik ein und bei weiteren Gelegenheiten auf andere. Aber keine Sorge, ich werde sicher nicht die super viel Mathematik-Zeugs reinpacken. So wie beim letzten Mal etwa. Das nächste Mal sehen wir uns wieder entweder auf Discord, oder bei meinem nächsten Beitrag, der über SpaceXs neue Mission handeln wird. Also … fangen wir mal an!
Mit den Formeln war alles okay soweit. Man konnte zuverlässig Planetenbahnen über Jahrzehnte hinweg bestimmen und für die meisten reichte es auch schon. Es war nämlich bereits eine sehr gute Näherung, wenn man die Keplerschen Gesetze zu Hand nimmt, um alles Wesentliche zu berechnen. Selbst die leichte Ellipsenform aller Planeten (inklusiver der Erde) und die deswegen auftretenden Geschwindigkeitsschwankungen konnten durch die Gesetze schon berücksichtigt werden. Aber wenn wir uns den Merkur anschauen, oder für Raumfahrtmission so energieoptimiert wie möglich denken müssen, dann merken wir, dass da was nicht passt. Aber schauen wir uns mal die Aufzeichnung, die auf speziell unser Himmelsmechanik-Problem von heute bestimmt sind (bzw. auch welche, dessen Aufzeichnungen über deren Beobachtung die Ursache eigentlich die Apsidendrehung ist, und nicht, wie früher öfters gedacht, etwas anderem zuzuschreiben sind)
Geschichte der Apsidendrehungsforschung
So wirklich ging es mit der Geschichte über die Forschung der Apsidendrehung im 9tem Jahrhundert. Thabit ibn Qurrah bemerkte, dass sich das Sonnenapogäum (Der Punkt in der Ekliptik (scheinbare Sonnenbahn um die Erde), an dem sich die Sonne am langsamsten bewegt, was aber auf die tatsächliche Erdbahn zurückzuführen ist) rechtläufig bezüglich der Äquinoktialpunkte (Der Ort, an dem sich die Sonne während einer Tagundnachtgleiche sich befindet) bewegt. Er hielt es allerdings für rein präzessionsbedingt (Präzession = (hier) Pendelbewegung der Erde um ihre Rotationsachse), wie auch alle vor ihm, die sich dieser Thematik näherten. Al-Battani empfahl für die Berechnung der Apogäumslänge denselben Betrag wie bei der konstanten Präzession zu seinem Ergebnis durch seine Beobachtung am 01. März 880, welches Ergebnis 82° 15′ ekliptikale Länge betrug, hinzu zu addieren. Sie bestimmten die Geschwindigkeit der Sonnenapogäumsdrehung, wie die Präzession der Erdachse auf 23 780 Jahren pro Vollkreis (Die Präzessionsbewegung dauerte tatsächlich J2000.0 25 784 Jahre pro Vollkreis). Und genau das verarbeitete Ptolemäus schon Jahrhunderte vorher in seinem Almagest ein.
Erst ibn asch-Shatir stellte im 14ten Jahrhundert fest, dass die rechtläufige Bewegung relativ zu den Äquinoktien doch eine andere Geschwindigkeit als die Präzession hat und also wohl nicht damit zusammenhängt.
Bevor wir zum Höhepunkt der Apsidendrehungsforschung kommen, möchte ich noch erwähnen, dass die Babylonier bereits die Perigäumsdrehung des Mondes kannten und sie in ihre Berechnungen mit einbezogen haben, was die Griechen übernommen und u.a. für die Epizykeltheorie weiterverwendet haben.
Periheldrehung des Merkur
Wir haben schon die Elliptizität der Planeten festgestellt. Durch Kepler beschrieben, begründet durch Newton. Wir haben auch schon erwähnt, dass Newton auch ermöglichte, die Bahnstörungen zu beschreiben, die die Planeten sich gegenseitig zufügen, auch wenn sie gleichzeitig nur sehr gering ist. Ebenso kann hierdurch die Apsidendrehung nahezu vollständig erklärt werden.
Wenn wir zurück mittig ins 19te Jahrhundert blicken, benutzte Urbain Le Verrier (einer derjenigen, die die Entdeckung des Neptuns maßgeblich vorangetrieben hat) für eine exakte Vermessung der Merkurumlaufbahn Daten aus Merkurtransiten und entdeckte, dass nach den himmelsmechanischen Berechnungen er sich etwa 40″ nicht von den (moderner Wert: 571,91″ je Jahrhundert) erklären konnte, was immerhin ein recht großer Betrag darstellt. Da er bereits erfolgreich unerklärliche Bahnstörungen von Uranus auf einen vorerst unbekannten Planeten, später den Neptun, schob, kam er zu dem Schluss, dass jetzt ein weiterer Planet innerhalb der Merkurbahn liegen müsste. Dieser Planet hielt ohne Entdeckung bereits den Namen „Vulkan“, aber konnte nie bei umfangreichen Suchen in der Nähe der Sonne, sowie bei einigen Sonnenfinsternissen gefunden werden. Daher spekulierten Wissenschaftler auf merkurnahe Asteroidengürtel, oder dem interplanetaren Staub selbst, aber mit ihren Erklärungsversuchen blieben alle auf der falschen Spur.
Bevor Einstein ins Spiel kam, versuchte Paul Gerber 1898 aus den elektrodynamischen Kraftgesetzen und unter der Annahme, dass sich die Gravitation mit Lichtgeschwindigkeit ausbreitet, diesen bislang unerklärlichen Überschuss abzuleiten. Seine Formel für diese Apsidendrehungsabweichung war tatsächlich identisch mit denen, die Einstein später aufgestellt hatte, aber leider waren die Kraftgesetze, die er angewandt hat, fehl am Platz und solch artige Theorie mussten aufgegeben werden. Einstein hatte dann aber mit seiner Allgemeinen Relativitätstheorie einen Erfolg verbucht, denn er konnte bis dato unwiderlegt und überzeugend diesen Überschuss erklären. Es war für die ART einer der ersten wichtigen Bestätigungen. (Berechneter Überschuss mit der ART: 42,98″ je Jahrhundert) Die Ursache des relativistischen Effekts liegt in der ganz leichten Abweichung zum klassisch invers-quadratischem Verhalten der Gravitation.
Damit ist es aber noch nicht getan, noch sind die Zweifel daran, dass die ART diesen Überschuss wirklich erklärt, nicht getilgt, denn die Apsidendrehung, die die rotationsbedingte Abplattung der Sonne hervorruft, konnten noch nicht mitberechnet werden. Jahrelang waren die Werte von der Größe der Abplattung der Sonne in sich widersprüchlich und somit blieb an der Erklärung des Überschusses von diesem Phänomen immer Angriffsfläche gegen die ART erhalten. Inzwischen kennt man den Wert der Abplattung zuverlässig und relativ genau und die Apsidendrehung, die die Abplattung verursachen kann beläuft sich auf nur wenige Hundertstel Bogensekunden.
Die Physik
Die Satelliten im Erdorbit erfahren eine Perigäumsdrehung durch die Abplattung der Erde. Im LEO kommt noch die Reibung an der Atmosphäre hinzu. So beträgt die Perigäumsdrehung der GPS-Satelliten, welche in einer Höhe von ca. 20 200 Kilometer um die Erde kreisen, etwa 0,01° pro Tag. Und hier kommt auch schon die Formel dafür:
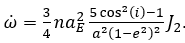
Dabei ist ω̇ die Apsidendrehung in Bogenmaß pro Umlauf, n die Mittlere Winkelgeschwindigkeit eines Satelliten auf seiner Umlaufbahn, aE die große Halbachse vom Äquator des zu umkreisenden Planeten, a die große Halbachse der Satellitenumlaufbahn, i die Inklination der Umlaufbahn gegen den Planetenäquator, e die Exzentrizität der Satellitenumlaufbahn und J2 der Entwicklungskoeffizient des Quadrupolmoments des Gravitationspotential des zu umkreisenden Planeten. J2 ist im Falle der Erde 1,082 635 9 × 10-3. Man rechnet n aus, indem man die Umlaufszeit durch den Vollkreis dividiert. Nehmen wir mal für unser Beispiel die ISS. Die Daten für die ISS a = 418,5 km; i = 51,6412°; n = , ca. 0,001 126 255; aE = 6 378 137 m; e = 0,000 124 9; J2 = 1,082 635 9 × 10-3. Also ist die Apsidendrehung der ISS in Bogenmaß pro Umlauf


Bei 15,493 901 88 Umläufen pro Tag macht das eine rechtläufige Periheldrehung von 2,387 330 911 507 135 Bogensekunden am Tag. Ich denke aber mal, fernab von wesentlich komplizierteren Rechnungen gerechnet zu haben, dass die Atmosphäre und der Sonnenwind fast eine größere Auswirkung haben könnten.
Wenn die Umlaufbahn eines Satelliten eine Inklination von ca. 63,4° gegen den Planetenäquator hat, dann ist das Perigäum näherungsweise stabil, unter 63,4° bewegt es sich rechtläufig, über 63,4° rückläufig. Diese Eigenschaft wird für einen besonderen Orbit benutzt, zu dem wir wann anders mal zurückkommen. Ein durchaus bedeutender Anteil der Apsidendrehung, insbesondere bei der Periheldrehung vom Merkur, wie wir weiter oben festgestellt haben, ist der relativistischer Anteil. Der kommt von der ART und von der Gravitation, welche ja nicht ganz invers-quadratisch sich auswirkt, und bei besonders hohen Geschwindigkeiten den Raum, bzw. die Zeit beeinflusst. So kann es grob gesagt sein, dass der Satellit minimal schneller ist, wenn er bereits schnell ist und, dass deswegen auch nur das Perihel, bzw. die Periapsis, sich dreht (und damit die Apsidenlinie und die Ausrichtung der Umlaufbahn, weswegen wir die Apsidendrehung in Winkelmaßen angeben). Die Formel dazu habe ich auch:
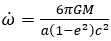
Das G ist die Gravitationskonstante (G = 6,6743 × 10-11), M die Masse des zu umkreisenden Objekts (Die Sonne (bei einem Planeten), der Planet (bei einem Mond/Satellit)) und c die Lichtgeschwindigkeit (per definitionem 299 792 458 m/s2). Nehmen wir doch für unser Beispiel dieser Formel den Merkur: (man braucht eigentlich nicht mit unglaublich vielen Nachkommastellen rechnen)
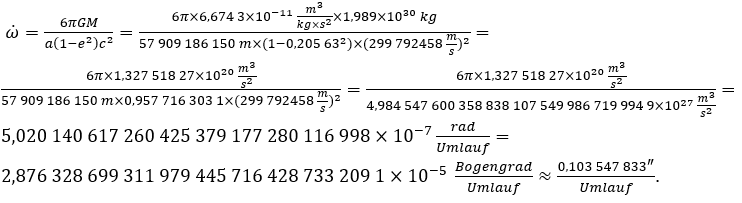
Das Perihel des Merkurs bewegt sich prograd (rechtläufig). Das ist eine Apsidendrehung von
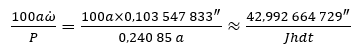
mit einer Umlaufszeit von Merkur von 0,240 85 Jahren. Das sind fast 88 Erdtage.
Ich hoffe, ich habe euch nicht zu mathematisiert. Keine Sorge, viel komplizierter als die Apsidendrehung habe ich nicht vor, was auf GSA zu machen. Außerdem wollte ich noch den Hinweis geben, dass ich bei der Beispielrechnung um die ISS nicht keine Gewähr auf absolute Korrektheit geben kann, auch wenn ich mir ziemlich sicher um meine Rechnung bin. Verzeiht mir, wenn ich mathematisch teilweise informal bin.
Quellen:
- Kompendium der Astronomie, Hans-Ulrich Keller, Kosmos, 2019, ISBN 978-3-440-16276-7, Kapitel 3 und S. 163
- https://de.wikipedia.org/wiki/Apsidendrehung
- https://farside.ph.utexas.edu/teaching/celestial/Celestial/node93.html
- https://www.heavens-above.com/orbit.aspx?satid=25544&lat=0&lng=0&loc=Unspecified&alt=0&tz=CET (Die ISS auf Heavens-Above)

Wonderful beat ! I would like to apprentice while you amend your web site, how can i subscribe for a weblog site?
The account helped me a appropriate deal. I had been a little bit familiar of this your broadcast offered shiny transparent idea
What? I don’t know about weblog. 😀
Hi there would you mind sharing which blog platform you’re working with?
I’m looking to start my own blog soon but I’m having a hard time making a decision between BlogEngine/Wordpress/B2evolution and Drupal.
The reason I ask is because your design seems different then most blogs and I’m
looking for something completely unique.
P.S Sorry for being off-topic but I had to ask!
This is a more-or-less standard WordPress website in terms of design. I like it because it is sufficient for what this website needs. The Theme is Twenty Sixteen if you want to play around with it. 🙂
Thank you for your question.
I think this is one of the most vital info for me.
And i’m glad reading your article. But wanna remark on few general
things, The website style is perfect, the articles is really
great : D. Good job, cheers