Tut mir leid. Ich weiß, ihr musstet schon wieder knapp über 3 Monate auf einen neuen Artikel warten. Aber ich hoffe, dass euch diese über 8 Tsd. Wörter wieder aufmuntern werden. 🙂
Einleitung
Unsere Weltkugel, auf der wir leben, das ist die Erde, ist zwar nicht ganz rund, sondern eher sphäroidal und am Nordpol etwas mehr gespitzt als in den meisten anderen Breitengraden und am Südpol sogar leicht eingedellt. Also nur, wenn man annehmen würde, dass die Erde nicht wegen der Rotation der Erde am Äquator um einige Kilometer dicker ist als an den Polen. Das liegt daran, dass die Erde durch die Rotation eher eine Art Rotationsellipsoid ist.
Nun, was könnte man jetzt machen, wenn man diese Fakten nutzen will, um zum Beispiel herauszufinden, wo ein ganz bestimmter Ort auf der Erde liegt? Genau, man könnte ein Gradnetz über die Erde spannen, denn dann könnte man in diesem Bezugssystem genau sagen, wo etwas liegt. Was ist unser Bezugspunkt? Nun, um am besten mit dem Gradnetz auch noch rechnen zu können, legen wir einfach fest, dass die zwei Richtungen, in die die Rotationsachse der Erde zeigt, die Pole unseres Gradnetzes sind. Was kann man damit rechnen? Wenn die Erde 23 Stunden 56 Minuten und 4 Sekunden für eine Rotation braucht, bzw. genau 24 Stunden von Mittag bis Mittag, und wenn wir die Erde in 360 Linien einteilen, die die beiden Pole verbinden, kann man sagen, dass wenn ein Beobachter 15 Grad östlich und auf gleicher Höhe von mir steht, dass bei ihm die Sonne eine ganze Stunde früher untergehen wird und auf meiner Position eine Stunde später wieder aufgehen wird als der Beobachter 15 Grad östlich von mir. So kann man auch sagen, dass wenn ich genau auf dem Äquator stehe, dass ich beobachten kann, wie die Sonne innerhalb eines Jahres immer wieder ihre Positionen einnimmt, die sich nur sehr langsam über die Jahre sich ändern, wobei ihr Kurs fast haargenau sich nach einem Jahr wiederholt. Ich kann auch auf dem Äquator beobachten, dass wenn die Tageslänge der Nachtlänge gleicht, dass die Sonne mittags genau über mir stehen muss, und das passiert sogar zweimal im Jahr. Im Gegenzug kann ich im Sommer in einer Polarregion die Sonne den ganzen Tag über sehen, ohne dass die Sonne untergehen wird. Auch wird sie dort im Winter nicht aufgehen und der Himmel wird abhängig von der Polnähe maximal nur zur Mittagszeit aufdämmern.
Leichter mit der Positionenbestimmung mithilfe eines Gradnetzes ist es, wenn man ein zusätzlich praktisches Gradnetz hat. Woran denke ich? … Genau! An den Fixsternhimmel. Ich beobachte den Himmel selbst seit ungefähr 10 Jahren mehr oder weniger aktiv und kann sagen, dass sich der Sternhimmel seitdem sich nicht verändert hat, zumindest insofern, dass ich mit dem Auge und ohne spezielle Methoden in der Hinsicht es nicht wahrnehmen würde. Tatsächlich bewegen sich auch die Fixsterne, also die Sterne, die vermeintlich fix am Himmel stehen, auch relativ zu uns. Zwar sind sie viele Billiarden Kilometer weit weg und bewegen sich nur mit wenigen Kilometern pro Sekunde relativ zu uns, aber im Laufe eines Jahres kann man in leistungsstarken Teleskopen erkennen, dass sie um wenige Millibogensekunden am Himmel verrückt sind. Eine Millibogensekunde ist der Tausendste Teil einer Bogensekunde, die wiederum der 60te Teil einer Bogenminute ist, die wiederum der der 60te Teil eines Bogengrades ist, wovon es wiederum 360 Bogengrad im Vollkreis gibt. Also ist eine Millibogensekunde der (1000 × 60 × 60 × 360) 1 296 000 000te Teil einer Bogensekunde. Übrigens sind diese Skalen auch ziemlich das Hochauflösendste, was wir an Teleskoptechnik im sichtbaren Licht gegenwärtig erreichen können.
Wenn also der Fixsternhimmel ziemlich fest ist, aber wir interessanterweise passend zum Tageszyklus und zum Jahreszyklus einen Nachthimmel sehen, der die Geschehnisse des Jahres und des Tages auch erklären können, sowie innerhalb dieser 23 Stunden 56 Minuten und 4 Sekunden den gleichen Fixsternhimmel vorfinden, liegt es irgendwie nahe, dass sich der Himmel nicht im Laufe eines Tages sich bewegt, sondern die Erde und als Beobachter auf der Erde zu den verschiedenen Tageszeiten einen anderen Teil des Himmels sehen können. Am Äquator, an dem wir sehen, dass sich die Sonne an den zwei Tagundnachtgleichen sich genau in einer senkrechten Linie von West nach Ost über den genauen Punkt über mir am Himmel sich bewegt, können wir nachts sehen, dass sich auch der Sternhimmel zwar zu jeder Zeit sich wie die Sonne an den Tagundnachtgleichen verhält.
In Verbindung mit einer Weltkarte und etwas meteorologisches Hintergrundwissen, kann anhand des Koordinatennetzes der Erde auch präzise die Meeres- und Windströmungen durch Corioliskräfte in der Atmosphäre und dann daraus entstehenden Hadley-Zellen und anderen Windsystemen vorhersagen, woraus sich wiederum eine ziemlich präzise Klimakarte in Verbindung mit Höhendaten der Kontinente erstellen lässt.
Koordinatensystem in der Himmelskugel
Bevor ich alles in der Einleitung schon verrate, fange ich schonmal lieber an, die Einleitung zu verlassen. Zuerst: Ja, wir haben ein wundervolles Koordinatensystem auf der Erde, und damit kann man wirklich was anstellen, und ja, wir können auch eins auf den Sternhimmel projizieren, aber es ist nicht die ganze Wahrheit. Dahinter ist noch etwas mehr Wissenswertes.
Der erste große Unterschied ist, dass wir von draußen auf die Erdkugel draufschauen, während wir vom Inneren der Himmelskugel auf ihre Oberfläche schauen. Klar, wenn auf der Erde wir gerade nach Westen schauen, dann schauen wir auch am Himmel nach Westen, genauso wie wenn wir nach Norden, Osten oder Süden schauen. Das ist zwar einfach zu verstehen, aber nicht zu vergleichen mit einem Globus von der Erde zum Beispiel.
Die Breitengrade nennen wir hier Deklination und die Längengrade Rektaszension. Es gibt einen kleinen Unterschied, wir haben bei der Deklination zwar von 90 Grad Süd bis 90 Grad Nord, aber bei der Rektaszension werden 24 Stunden gezählt, die wiederum in Minuten und Sekunden und so weiter aufgeteilt sind.
Das ist ziemlich nützlich, denn so kann man leichter abschätzen oder berechnen, zu welcher Tages- und Jahreszeit ein Stern auf- oder untergeht. Am Frühlingspunkt haben wir 0h Rektaszension, also wenn die Sonne den Himmelsäquator (Deklination: 0 Grad) streift, das ist jeweils am 20/21. März des Jahres momentan. Etwa zwei Wochen später liegt die Sonne schon auf 1h, nach einem Monat auf 2h. Bei 6h ist Sommersonnenwende (also, wenn die Sonne am nördlichsten am Himmel steht), bei 12h ist wieder Tagundnachtgleiche, aber dafür im Herbst und Sonne auf 18h, das bedeutet dann Wintersonnenwende. Somit sieht man den Himmelsausschnitt gerade am besten, der zu Mitternacht und 12h Rektaszension der Sonne gegenübersteht. Also z.B., wenn am 01. Februar die Sonne noch auf etwa auf 20h46 steht, dann sieht man die Region um 8h46 Rektaszension nachts am besten, und zwar in südlichster Richtung gegen Mitternacht.
Die Deklination wird mit Delta δ und die Rektaszension mit Alpha α abgekürzt. Dieses Koordinatensystem für den Himmel wird als geozentrisch und äquatorial betrachtet, weil z.B. ja der Punkt über einen, wenn man genau sich auf dem Erdäqutor befindet, dass dann auch der Himmelsäquator präzise über einen entlangläuft.
Für Objekte des Sonnensystems werden auch gerne mal ekliptikale Koordinaten angegeben. Dann ist der Äquator in diesem Koordinatensystem die Ekliptik, also die scheinbare Sonnenbahn um die Erde und der Meridian, also der Nullpunkt der Längengrade/Rektaszension, ist dann meist auch der Frühlingspunkt, oder immer die Sonne selbst. Im ersten Fall sieht man die normalen Planetenbewegungen und Abweichungen von der Ekliptik im einstelligen Gradbereich, im zweiten Fall sieht man eigentlich nur die Abstände zur Sonne und damit auch ganz gut die Sichtbarkeit der Planeten.
Fernerhin gibt es dann auch das Galaktische Koordinatensystem, wo dann das Milchstraßenband ähnlich der Ekliptik fungiert und der Meridian auf dem Supermassiven Schwarzen Loch liegt. Sterne der Milchstraße werden gerne auch noch mit diesen Koordinaten aufgezeichnet.
Weil die Erde in ihrer Rotation und Revolution (Erde um sich selbst, Erde um die Sonne) etwas hin und her wobbelt, auch Präzession genannt (Wow, jetzt habe ich alle drei klassischen Bewegungsformen der Erde aufgelistet!), werden mit Koordinatensysteme nach der Epoche gearbeitet. Die heutige Standardepoche ist J2000.0 (Also Jahresbeginn von 2000), aber schon heute sind Veränderungen deutlich feststellbar. Zum Beispiel verändert sich die Rotation der Erde durch Massenströme im Erdinneren, die Revolution durch die Apsidendrehung zum Beispiel, und die Präzession ist ja eigentlich nur das alleinige Schwingen der Rotationsache der Erde. Die kostenlose und downloadbare Computersoftware Stellarium kann zum Beispiel Koordinatensysteme unabhängig von der Epoche „von jetzt“ berechnen.
Ein interessantes Merkmal ist, dass wenn ich hier auf 49° Nord Breitengrad sitze, dass ich alle Sterne oberhalb der 41° Nord Deklination praktisch immer sehen kann. Der Himmelspol ist dann irgendwo am Himmel, nicht am Zenit (der Punkt am Himmel direkt über dir, Nadir ist das Gegenteil) oder am Äquator, und somit bewegt sich der Stück des Himmels zwischen dem Horizont und dem Himmelspol nach einem halben Tag über den Himmelspol und nochmal einen halben Tag später steht die Region wieder am selben Fleck am Himmel, ohne unterzugehen. Diese Region am Himmel, in der dies zutrifft, ist deswegen kreisförmig, und unveränderlich, sofern man sich nicht bewegt. Diese Sterne sind dann zirkumpolar, sie werden nachts nicht unsichtbar werden (das kann man sich ähnlich wie die nie untergehende Sonne im Sommer hoch im Norden vorstellen).
Andererseits kann ich auf 49° Nord keine Objekte unterhalb von 41° Süd sehen (wenn der Horizont eben ist, keine Bäume oder Hügel im Weg stehen, die Atmosphäre es nicht verhindere…). Diese -41° Deklination wird auch nur Richtung Süden am Himmel erreicht. Auf der Nord-Süd-Linie sind auch alle Objekte am höchsten über dem Horizont und haben genau die Hälfte ihrer täglichen Reise am Himmel abgeschlossen. Die Nord-Süd-Linie deswegen, weil es ja quasi die Erdachse widerspiegelt.
Diese Schlüsse sind so möglich einfach wegen der Kugeleigenschaft der Erde. Auf einer Kugel sitzend sehe ich unter dem Horizont nur die Kugel und über dem Horizont den Himmel.
Wenn ich jetzt nicht gerade auf dem Äquator oder auf einen der beiden Pole sitze, sondern irgendwo anders, dann kann ich theoretisch eine erdachte Verlängerung von einem Pols sehen. Dieser Pol projiziert auf den Himmel ist der Himmelspol. Da die Erde ihre Rotation in vollen Zügen am Äquator hat und die Pole stillstehen und nur um sich selbst bewegen, quasi, kann man die erdachte Linie vom Himmelspol zum Äquator innerhalb eines Tages wieder am Ausgangspunkt beobachten. Der Himmel dreht sich mit, weil sich eigentlich die Erde dreht und wir somit nur die projizierte Bewegung am Himmel sehen können.
Helligkeiten in der Astronomie
Schon Ptolemäus in der Antike hat bereits die Sterne, die er katalogisiert hatte, in 6 Größenklassen eingeordnet. Diese Größenklassen haben zwar nichts mit der tatsächlichen Größe oder mit der Masse zu tun, aber mit der Helligkeit, mit der wir die Sterne sehen. Dabei ist die erste Größenklasse die hellste Sternkategorie gewesen.
Heute nutzen wir immer noch ein ähnliches System. Unser „Null“-Stern ist die Wega für gewöhnlich und richten dann die Helligkeiten nach ihr aus. Die Einheit wird einfach Magnitudo (lat.) genannt und bedeutet eigentlich ebenso „Größe“. Es wird mit m oder mag häufig abgekürzt. Je größer die Zahl wird, desto dunkler leuchtet der Stern. Deswegen kommen auch negative Werte für sehr helle Sterne vor.
Man unterscheidet verschiedene Arten von Helligkeiten:
- Die Scheinbare Helligkeit:
Die Scheinbare Helligkeit ist die reine Helligkeitsangabe mit mag, wie hell der Stern hier auf der Erde erscheint. Wenn ein Stern eine Helligkeit von +2,0 mag hat und ein anderer Stern hat eine Helligkeit von +7,0 mag, dann sind zwar 5 mag bei der Differenz in der Helligkeit der beiden Sterne, aber die Intensität des 2,0-mag-Sterns ist gegenüber dem 7,0-mag-Stern um den Faktor 100 stärker. Also ist das Verhältnis mit 5 Größenklassen Unterschied 1:100. Die Einheit mag ist dennoch regelmäßig und das Verhältnis der Intensität zur Helligkeit bei nur einer Größenklasse Unterschied ist bei 1001/5 = 2,511 886 431 509 580 111 085 032 067 799 3…. Das heißt, dass ein Stern von +2,0 mag um fast das 2,512-fache heller ist, als ein Stern mit +3,0 mag, und fast um das 6,310-fache heller als ein Stern mit +4,0 mag (1002/5). Es gelten also folgende Beziehungen zwischen Helligkeit und Intensität: m1 – m2 = –2,5 lg (l1/l2), bzw. l1/l2 = 10–0,4(m₁–m₂). - Absolute Helligkeit:
Alle Fixsterne und andere Objekte haben unterschiedliche Entfernungen und so kann es sein, dass ein hellerer Stern, der aber weiter entfernt ist als ein dunklerer Stern, dann scheinbar doch dunklerer ist als unser eigentlicher dunkler Stern.
Um das zu vermeiden, stellen wir uns jetzt vor, dass alle Sterne nun in einer bestimmten Entfernung stehen, sagen wir mal 10 Parsecs.
Während man die scheinbare Helligkeit mit einem m abkürzt, kürzt man die absolute Helligkeit mit einem M ab.
Wiederum kann man auch die Absolute Helligkeit über einen Logarithmus berechnen. Die Formel dafür ist: m – M = 5 × log10 (r/10 pc). Dabei ist M die Absolute Helligkeit, m die Scheinbare Helligkeit und r die Entfernung in Parsec. Mit dieser Formel ist nun sichergestellt, dass ein Stern in 10 Parsec Entfernung dieselbe Scheinbare Helligkeit wie die Absolute Helligkeit hat: m – M = 5 × log10 (r/10 pc) = 5 × 0 = 0. Also, wie man hier gut sehen kann, ist die Distanz von 10 Parsec per Definition unsere Distanz, auf die wir normen. Nehmen wir jetzt den Stern Polaris, der Polarstern, und setzen die bekannten Werte für Polaris ein, kommt folgendes heraus: 2,02 mag – M = log10 (132,6 pc/10 pc) ≈ 5 × 1,122 544 = 5,612 72. Daraus resultiert, dass die Differenz zwischen m und M 5,612 72 beträgt, was wiederum leicht für M umgeformt werden kann: 2,02 mag – M = 5,612 72 ⇒ M = –3,592 72 mag, also leicht weniger als -3,6 mag. Ein kurzer Blick in die Wikipedia, und man sehe, dass der Wert korrekt ist. - Bolometrische Helligkeit
Hast du dich schonmal darüber gewundert, für was für Wellenlängen eigentlich die Helligkeit jetzt stimmt? Nun, besonders für die Scheinbare Helligkeit werden gerne nur die Wellenlängen im visuellen Band genommen. Sterne haben aber verschiedene Helligkeiten in anderen Bändern. Das Spektrum eines Sterns nähert sich an die Plancksche Schwarzkörperstrahlung an. Ja, klar, die Sterne sind auch nicht ganz perfekt und irgendwelche Materialien werden elektromagnetische Wellen in bestimmten Bändern absorbieren, sodass der Energiestrom in dem Band stark zurückgeht. In der Bolometrischen Helligkeit versucht man nun die Helligkeit über das gesamte elektromagnetische Spektrum zusammenzufassen. Die Bolometrische Helligkeit wird in mag angegeben, aber auch des Öfteren in Watt oder in Erg pro Sekunde. Bei der Bolometrischen Helligkeit wird zwischen der scheinbaren und der absoluten unterschieden, da es ja kein wirkliches Gegenstück zur Scheinbaren oder Absoluten Helligkeit darstellt.
Konkret wird die Bolometrische Helligkeit seit 2015 in der Resolution B2 über eine Leistungskennzahl bestimmt und nicht mehr über die variable Leistung der Sonne. Die Formel für die Bolometrische Helligkeit ist: Mbol = –2,5 log10 (L*/L0). L0 ist die Normgröße für die Bolometrische Helligkeit und wurde auf 3,012 8 × 1028 Watt festgelegt. Durch die Solarkonstante L* von 1 361 W/m² strahlt die Sonne gesamtflächig 4π × (149 597 870 700 m)2 × 1 361 W ≈ 3,826 661 × 1026 W aus. Das in die obere Formel eingesetzt, ergibt Mbol = –2,5 log10 (3,826 661 × 1026 W/3,012 8 × 1028 W) ≈ 4,74 mag, während die Sonne im sichtbaren Licht nur eine Bolometrische Helligkeit von +5,16 mag aufweist. - Leuchtkraft
An der Bolometrischen Helligkeit ist die Leuchtkraft angeknüpft. Sie drückt die wahre Leuchtkraft aus, so wie wir schon in der Bolometrischen Leuchtkraft damit gerechnet haben. Jedoch ohne die Magnitudenskala, sondern reine Werte. Man rechnet meistens mit Sonnenleuchtkräften. Eine Sonnenleuchtkraft beträgt 3,828 × 1026 Watt, ein Stern mit zwei Sonnenleuchtkräften hat zweimal mehr Leistung als die Sonne. Da unsere Sonne eher im Mittelfeld der Sterne spielt, gibt es viele Sterne, die nur einen Bruchteil der Leuchtkraft der Sonne haben, andere wiederum bis über 100 Tausend Sonnenleuchtkräfte. Allerdings kann man keine Roten Zwerge, noch nicht einmal der 4,24-Lichtjahre entfernte Proxima, aus unserer Position heraus mit dem bloßen Auge sehen, während wir Typ-I-Hyperriesen Tausende Lichtjahre weit sehen können.
Zeitmessung in der Astronomie
Die Menschen wollten schon immer wissen, zu welcher Jahreszeit sie ihre Felder bestellen oder ihr Angepflanztes ernten sollten, wann sie etwa Fluten oder Regenzeiten und Stürme erwarten sollten, wie der Tagesablauf vom Sonnenaufgang bis zum Sonnenuntergang über den Mittag und der Nacht ging. Dies war und ist ja praktisch, denn so kann man sich seine Zeit besser einplanen, oder vielleicht sogar Berechnungen machen.
Am einfachsten ist es, die Jahreszeiten und Tageszeiten an definitiv wiederkehrende Phänomene auszurichten und genauer zu bestimmen. Während eines Tages dreht sich die Sonne von Ost nach West, in der Nacht dreht sich dafür der Sternenhimmel. Jahresweise verändert sich die Höhe der täglichen Sonnenbahn und verschiedene Sternbilder kann man im Laufe eines Jahres immer später in der Nacht sehen. An solchen Regelmäßigkeit knüpften alle Zeitsysteme, die auf der Erde erschaffen wurden.
Einige schlaue Köpfe konnten die Kalendarisierung der Zeit im Laufe der Jahrhunderte vorantreiben. Bereits die alten Kulturen konnten die Länge eines Tages oder die Länge eines Jahres präzise auf einige Nachkommastellen berechnen. Das ist wichtig für die Erstellung der Kalender.
Der Tag
Allerdings ist auch wichtig zu wissen, was genau ein Tag oder ein Jahr eigentlich ist. Es ist eine unterschiedliche Messung, wenn man die Zeit zwischen Sonnenaufgang bis Sonnenaufgang misst, oder von Aufgang eines Fixsterns bis zum nächsten Aufgang desselben. Deshalb werden wir mal einen genaueren Blick zuerst auf die unterschiedlichen Messungen eines Tages annehmen. Ein etwas fachspezifischerer Begriff für den höchsten Stand am Himmel eines Himmelsobjekt in seiner Laufbahn ist die Kulmination. Folgerichtig kulminiert die Sonne zum Beispiel immer mittags, da sie am Mittag immer am höchsten am Himmel steht. Zur selben Zeit steht sie übrigens genau in Richtung Süden.
- Wahrer Sonnentag:
Der Wahre Sonnentag ist die zeitliche Differenz zwischen zwei Kulminationen der wahren Sonne. - Mittlerer Sonnentag:
Ein Mittlerer Sonnentag ist praktisch der Wahre Sonnentag, bloß eine gemittelte Form von vielen Sonnentagen. Per Definition sind 86 400 Sonnenzeitsekunden ein Mittlerer Sonnentag. 60 Sekunden sind eine Minute, 60 Minuten sind eine Stunde und es gibt 24 Stunden. Ein Mittlerer Sonnentag sind auch 24 Stunden, 3 Minuten und 56,555 Sternzeitsekunden. - Wahrer Sterntag:
Der Wahre Sterntag ist die Zeit zwischen zwei Kulminationen des Frühlingspunktes. Der Frühlingspunkt ist wie schon gesagt, der Sternort, an dem die Ekliptik, die Sonnenbahn, den Himmelsäquator kreuzt. Er ist auch gleichzeitig die Nullrektaszension und die Position der Sonne am 20/21.03 eines Jahres der aktuellen gregorianischen Zeitrechnung. - Mittlerer Sterntag:
Der Mittlere Sterntag ist die Zeit zwischen zwei Kulminationen des mittleren Frühlingspunktes. Ein Wahrer Sterntag sind per Definition 86 400 Sternzeitsekunden. 60 Sekunden sind eine Minute, welche 60 davon wiederum eine Stunde ergeben und es 24 Stunden gibt. Auch sind 23 Stunden, 56 Minuten und 4,091 Sekunden der Sonnenzeit ein Wahrer Sterntag. - Siderischer Tag:
Das ist die Zeit zwischen zwei aufeinanderfolgenden Kulminationen eines Fixsterns mit verschwindender Eigenbewegung. Er ist lediglich 9 Millisekunden länger als ein Mittlerer Sterntag.
Was sind die Unterschiede der einzelnen Sichtweisen für einen Tag? Mittlerer ~tag bedeutet zum Beispiel immer, dass eine große Zahl von echten ~tagen genommen wurden und der Durchschnitt dann als Maß genommen wurde. Die Abweichungen sind messbar, jedoch nicht unmittelbar wichtig für den normalen Alltag. Der Unterschied zwischen Sterntag, bzw. Siderische Erdrotation und Sonnentag ist schon größer. Der Sonnentag ist ein wenig länger als die anderen Tage, da von Mittag bis Mittag gemessen wurde. Da aber die Sonne während eines Erdtages sich in dieselbe Richtung wie die Erde bewegt, muss man am Ende eines Sterntages noch die Rotationszeit miteinbeziehen, die man braucht, um die scheinbare Eigenbewegung der Sonne zu kompensieren.

Innerhalb eines Sonnentages dreht sich die Erde also ihre gewöhnliche 360 Grad, plus bisschen mehr als ein ganzer Grad dazu, weil die Erde sich in ihrem Umlauf schon etwa um einen 365ten Teil um ihre Bahn um die Sonne sich gedreht hat, und somit winkeltechnisch sich in der Position zur Sonne mit der Ausgangsposition sich bewegt hat. Am besten hier mit der Grafik visualisierbar.
Bei Siderischer Tag und Sterntag geht es auch noch um die dritte Erdbewegung, die Präzession. Der Sterntag berücksichtigt die Präzession, die Siderische Rotationsperiode nicht. Also, damit ist gemeint, dass der Sterntag die Kulmination eines festen gedachten Punkts am Himmel anzeigt, aber der Siderische Tag bezieht ich auf den Sternenhintergrund, der sich mit der Präzession schwach und fortlaufend verschiebt.
Direkt beobachtbar sind nur die Wahren Sonnen- und Sterntage, sowie die Siderische Rotation, die gemittelten Tage sind nur mathematisch. Unser System, welches wir benutzen, ist das Sonnentagsystem.
Das Jahr
Das irdische Jahr kann man jeweils auch mit verschiedenen Definitionen betrachten, es gibt drei Überkategorien. Zu den klassischen Definitionen gibt es allerdings noch ein paar andere.
Das Sonnenjahr
Beim Sonnenjahr, also die Kalenderrechnung an die Sonne angepasst, sodass man auch leicht die Jahreszeiten im Kalender berücksichtigen, gibt es hauptsächlich drei verschiedene Zählungen:
- Siderisches Jahr:
Das siderische Jahr funktioniert analog zum Sterntag; das ist eine Umdrehung der Erde um die Sonne, genommen ist als fester Bezugsrahmen der Fixsternhimmel. Die durchschnittliche Dauer hier sind 365,256 363 004 Tage, oder 365d06h09min09,764sec. 365,256 360 416 7 Tage zur Epoche J2000,0. Das ist quasi die „vollständige Umkreisung“. - Tropisches Jahr:
Das tropische Jahr funktioniert analog zum Sonnentag; beim tropischen Jahr nimmt die mittlere Länge der mittleren Sonne um genau 360° zu. Als Ausgangspunkt wird der Frühlingspunkt genutzt, also ist die Definition die Differenz von zwei mittleren Durchgängen des Frühlingpunkts. Aufgrund der Präzession der Erde, das ist eine leichte Taumelbewegung der Erdachse über den Himmel, ist das tropische Jahr etwa 20 Minuten und 24½ Sekunden kürzer als das siderische Jahr. Dadurch, dass die Erdachse wandert, wandert auch der Frühlingspunkt langsam mit. Also respektiert diese Definition die Jahreszeiten. Seine Länge ist hier 365,242 190 53 Tage, oder 365d05h48min45,262sec. - Anomalistisches Jahr:
Das anomalistische Jahr ist eine Umdrehung der Erde um die Sonne, wobei die Zeit zwischen den Periheldurchgänge gezählt wird. Das Perihel oder Perihelion ist der nächste Punkt zur Sonne auf der Erdumlaufbahn. Da sich das Perihel langsam auf der Erdumlaufbahn sich ebenso mitbewegt, haben wir hier ein Jahr fünf Minuten länger als das siderische, also ist die Dauer durch diese Definition 365,259 635 864 Tage oder 365d06h13min52,539sec zur Epoche J 2000,0.
Weiterhin gibt es zwei große Solarkalender, die in der Welt existieren. Der julianische und der gregorianische. Beim julianischen Jahr ist es so, dass es 365 Tage im Jahr gibt, sowie 12 Monate mit jeweils 28 bis 31 Tage im Jahr. Alle vier Jahre kommt ein Tag dazu. Dass macht also ein mittleres Jahr von 365,25 Tagen. Das ist nicht allzu genau und bedeutet man braucht fast 900 Jahre, damit der Frühlingsanfang sich um eine Woche nach hinten verschiebt. Beim Gregorianischen Kalender (das ist auch übrigens der, den wir nutzen, orthodoxe Christen nutzen den Julianischen Kalender) gibt es zu den bereits getroffenen Regeln noch die Regel, dass das 00er-Jahr eines Jahrhunderts keinen Schalttag hat, es sei denn, es ist das vierte Jahrhundert. Das heißt im Klartext, 2000 ist zwar ein Schaltjahr, weil es durch 400 teilbar ist, 2100 jedoch nicht. Das macht dann ein mittleres Jahr von 365,2425 Tagen. Nach 22 619 Jahren wäre erst der Frühlingsanfang um eine Woche verschoben. Das Gregorianische Jahr geht also um 26,7 Sekunden pro mittleres Jahr falsch. Mittleres Jahr immer, weil man keine teilweisen Schalttage haben will. Das mittlere Jahr ist somit einfach ein Mittel aus allen Jahren in einem Abschnitt eines wiederholenden Segments. Weil ein Zyklus 400 Jahre dauert, das ist wegen der höchsten Regel, ist es in der Perspektive von ein paar Jahrzehnten ungenauer, was dazu führt, dass jedes Jahr die Tendenz sogar ist, dass das Datum des Frühlingsanfangs sogar geringfügig rückläufig ist.
Bei diesen Kalendern gibt es auch Wochen und Monate, aber eigentlich nur, um das Jahr nochmals aufzuteilen, bzw. sieben Tage in eine Art Bündel zu packen.
Der Julianische Kalender wird besonders in der Astronomie bei den Ephemeriden genutzt. Genannt ist dies das Julianische Datum (JD), welches mit Beginn auf den Mittag des 1. Januar 4713 v. Chr. gelegt wurde. Das System ist einfach eine simple Tageszählung, was bedeutet, dass der 01.01.2000 JD 2451545,0 ist. Die Uhrzeit für …,0 ist allerdings 13:00 Uhr MEZ, weil ab Mittag in der UTC-Zeitzone in der Rechnung ein neuer Tag beginnt (MEZ, Mitteleuropäische Zeit liegt eine Stunde nach UTC; UTC+1). 13 Tage sind es jedoch weniger, wenn man jetzt die Tage ausrechnen würde. Das lässt sich aber damit erklären, dass 10 Tage im Rahmen der Einführung des gregorianischen Kalenders gestrichen wurden, sowie auch drei Schalttage in den Jahren 1700, 1800 und 1900.
Es gibt auch das MJD, wie ihr euch schon vorstellen könnt, dass ist das Modifizierte Julianische Datum. Das MJD ist vom Konzept her das JD, bloß 2 400 000,5 Tage weiter. Das wäre dann der 17. November 1858 genau um Mitternacht nach UT natürlich. Niemand will wirklich das MJD verwenden, bis auf in der Raumfahrt, außerdem wäre es eigentlich nur extra Arbeit ein funktionierendes System nur in der Größenordnung der Zahlen etwas einzuschrumpfen.
Das Mondjahr
Genauso wie die Sonne ist auch der Mond ein geeignetes Medium, die Zeitmessung an ihm auszurichten. Physikalisch gesehen gibt es wieder verschiedene Definitionen, sowie eine Definition, die von den Kalendern am ehesten präferiert ist. Ein Mondjahr nennt man oft einfach Monat.
- Siderischer Monat:
Wie man es schon gedacht hat, auch hier ist die Zeitspanne, wie lange der Mond braucht, um wieder zur selben Stelle zurückzukehren, gemeint ist hier dieselbe Stelle im Referenzrahmen der Fixsterne. Und ein siderischer Monat beträgt somit in der Epoche J2000.0: 27,321 661 547 203 Tage, das sind 27d07h43min11,56sec. - Synodischer Monat:
Der synodische Monat ist für uns bei der Zeitrechnung mit dem Mond am wichtigsten. Das synodische Jahr ist die zeitliche Differenz von einer Mondphase zur allerselben. Zum Beispiel von Neumond zu Neumond. Dabei ist die Winkel Erde – Mond – Sonne wichtig. Auch bei anderen Planeten ist diese Definition des Jahres nicht uninteressant, weil so auch z.B. die Oppositionen, also die besten Sichtbarkeiten, ermittelt werden. Der synodische Monat wird auch Lunation genannt.
Ein synodisches Jahr dauert etwa 2,2 Tage länger als ein siderisches Jahr, da die Erde während eines Monats sich ja auch noch um die Sonne bewegt, und dadurch die Mondphasen etwas in die Länge zieht. Ein synodischer Monat beträgt zur Epoche etwa 29,530 588 853 1 Tage, das sind 29d12h44min2,877sec. Der synodische Monat variiert allerdings −0,259 d (6 h 12 min kürzer) bis +0,302 d (7 h 15 min länger) im aktuellen Intervall von 200 Jahren (genommen 1900 bis 2100) aufgrund von Bahnstörungen, welche Thema eines zukünftigen Eintrags werden. - Drakonitischer Monat:
Beim drakonitischen Monat wird die Zeit zwischen zwei Durchgängen des Mondes durch einer seiner Mondknoten gezählt, also zum Beispiel vom aufsteigenden Knoten zum nächsten. Aufsteigender Knoten und absteigender Knoten, das sind die Stellen, an die eine Umlaufbahn eine bestimmte Ebene durchkreuzt. Der Mond hat eine Inklination von 5,16 ° gegen die Ekliptik. Das bedeutet, dass die Mondbahn an zwei Stellen die Ebene der Ekliptik zu diesen 5,16 ° schneidet. Diese Schnittpunkte sind die beiden Knoten. Aufsteigend bedeutet, dass der Mond in den nördlichen Teil wechselt, absteigend andersherum. Auf 12 Monate gerechnet dauert die Periode etwa 326,546 64 Tage, also 27,212 220 Tage pro Monat, das sind 27d05h05min35,8sec. - Tropischer Monat:
Der tropische Monat hat in der Zeitrechnung mit dem Mond meist eine weniger wichtige Stellung. Im Bezug zum Mond ist das die Zeit, die er braucht, um vom Frühlingspunkt zum nächsten zu kreisen. Da durch die Präzession der Erde der Frühlingspunkt sich langsam leicht versetzt, ist diese Monatsdefinition fast gleichlang wie der siderische Monat. 27,321 582 Tage oder 27d7h43min4,7sec ist die Periode. - Anomalistischer Monat:
Analog zum Sonnenjahr ist der anomalistische Monat die Periode zwischen zwei Übergängen der Periapsis (nächster Punkt eines Himmelskörpers auf einer Umlaufbahn um ein Zentralobjekt), in dem Fall das Perigäum. Auch das Perigäum des Mondes wandert auf seiner Umlaufbahn entlang, was dazu führt, dass diese Periode sich auch etwas von dem siderischen Monat abhebt. Der anomalistische Monat dauert etwa 27,554 550 Tage oder 27d13h18min33,1sec.
Anders als beim Sonnenkalender ist der Mondkalender nur auf den Mond ausgerichtet. Ein Mondkalender muss demnach nicht zwingend den Sonnenlauf berücksichtigen. Der vermutlich bekannteste Mondkalender ist der islamische Kalender, oder auch Hidschri-Kalender genannt. Wie die meisten Mondkalender benutzt er die Mondphasen und eine komplette Lunation wird als Monat aufgefasst. Ein Monat hat wegen der Dauer des synodischen Monats (ca. 29,53059 Tage) in den allermeisten Fällen 29 oder 30 Tage. Der islamische Kalender bündelt zwölf Monate in ein Mondjahr zusammen, der allerdings 10 ⅞ Tage pro Sonnenjahr bereits ein neues Mondjahr beginnt. Der islamische Kalender nimmt dabei jedoch keine Rücksicht auf das Sonnenjahr.
In der Praxis ist der islamische Kalender uneinheitlich; verschiedene muslimische, islamische und arabische Gebiete oder Staaten benutzen ihre eigene Kalenderführung, wobei jedes Gebiet oder Staat ihre eigenen Astronomen haben, die vor einem Komitee jeden Monat von ihrer Sichtung des zunehmenden Mondes machen. Der neue Monat wird von den höchsten Stellen der jeweiligen Gebiete oder Staaten verkündet, und zwar nachdem der zunehmende Mond zum ersten Mal entdeckt wurde, also wenn er zum ersten Mal einer Lunation nach der Sonne untergeht.
Einige Staaten oder Gebiete nutzen dafür inzwischen Berechnungen oder einheitliche Regeln, allerdings ist die Gelehrtenwelt an dem Punkt verstritten. Alle Länder bis auf Iran und Afghanistan nutzen allerdings im Alltag auch den gregorianischen Kalender. In Iran und Afghanistan nutzen sie einen „islamischen“ gregorianischen Kalender: Auf den islamischen Kalender angepasst, aber im Grunde ein reiner Sonnenkalender mit ähnlichen Monaten wie unser gregorianischer Kalender. Der islamische Kalender wird in der islamischen Welt für gewöhnlich fast nur zu religiösen Anlässen verwendet.
Der Lunisolarkalender
Der Lunisolarkalender ist, wie der Name schon vermuten lässt, eine Mischung aus beidem. Die Monate sind ähnlich einem Mondkalender dem Mond angepasst, während die Jahre aber grundsätzlich nach der Sonne ausgerichtet sind. Das kann durchaus als Vorteil angesehen werden: Der Kalender, der nach der Sonne funktioniert erleichtert die Landwirtschaft und kann einfacher die Jahreszeiten und Wetterzusammenhänge aufzeigen, während die Monate nach dem Mond im selben Kalender für spirituelle Feste, Sonnen- und Mondfinsternisse und so Zeug erleichtern. Das hört sich gut an, kann jedoch gleich am ersten Punkt scheitern. Ein Mondmonat und ein Sonnenjahr haben zahlentechnisch kein Verhältnis zueinander. Wie will man einen funktionierenden Kalender erstellen, der die Sonne und den Mond zugleich berücksichtigt? Nun die erste Idee ist: Die beiden Zeitsysteme teilen sich zwar dasselbe Kalendersystem, sind aber unabhängig voneinander. Man hat im Grunde dann zwei Kalender, was wiederum schlecht funktioniert. Welchen Kalender benutzt man jetzt wann? Benutzt man beide gleichzeitig? Ist das dann aber nicht ein bisschen unnötig, weil es ein Kalender auch tun könnte? Die andere Idee ist, dass sie doch nicht unabhängig voneinander sind. Es gibt Mondmonate wie im Mondkalender, aber nicht immer 12 Monate sind zusammengefasst, sondern manchmal auch 13 Monate.
Das kann man gut demonstrieren. Ein synodischer Monat, solange dauert eine Lunation oder Mondmonat, dauert etwa 29,53059 Tage, während das tropische Jahr etwa 365,24219 Tage sind. Einige Lunisolarkalender nutzen das siderische Jahr, was aber bedeutet, dass diese Unterart nicht so gut die Jahreszeiten abbildet, sondern eher zu welchen Vollmonden der Mond in welches Sternbild eingetreten ist. 365,24219 Tage durch 29,53059 Tage sind etwa 12,368 266 Tage. Wobei 0,368 266 sehr arg an 7/19 erinnert, was 0,368 421 ist. Das bedeutet, dass man 7 Schaltmonate in 19 Jahr einbauen muss, welche sonst immer 12 Monate haben. Also 235 Monate in 19 Jahren. 235 Mondmonate minus 19 Sonnenjahre ist nur ein Unterschied von 2h04min56,1sec, wobei die 235 Mondmonate um diese Zeit länger sind als die 19 Sonnenjahre. Nach 12 mal dieser Epoche sind 2820 Mondmonate ähnlich viel wie 228 Sonnenjahre, aber bloß 25 Stunden weniger, und zwar ziemlich genau 25 Stunden weniger, tatsächlich sind es 24h59min13,2sec weniger als die Mondmonate in dem Verhältnis.
Eine andere Idee würde wieder bei den 12,368 266 Tagen starten. Statt 7/19 zu nehmen. Nehmen wir nun 123/334, wobei 0,368 263 herauskommt. Diese Zahl liegt nun schon viel näher an den 0,368 266 von weiter oben. Natürlich sind auch die Zähler und Nenner höher als bei 7/19. Wegen den 12,368 263, wir müssen ja die 12 hinzunehmen, da ja ein Sonnenjahr mehr als 12 Monate hat. Um herauszufinden, wie viele Mondmonate wie vielen Sonnenjahren hier gegenüberstehen, müssen wir einfach 334 mit 12 multiplizieren und dann mit den 123 addieren. Und ein Verhältnis von 4131 Mondmonaten zu 334 Sonnenjahren kommt heraus. Nach 4131 Mondmonaten sind etwa 121 990,862 552 Tage und nach 334 Sonnenjahren sind 121 990,891 637 Tage vergangen. Das macht einen Unterschied von 0,029 085 Tage, oder 41min52,9sec. Diesen marginalen Unterschied kann man mithilfe von Schalttagen in einer der Monate realisieren.
Diese fast 42 Minuten weniger alle 334 Sonnenjahre stellt einen über 52-fach genaueren Kalender dar als diese bisschen mehr als 2 Stunden alle 19 Jahre vom oberen Beispiel.
Wie man sieht, kann man diese Perfektion zur Spitze treiben, aber wie sähe ein Lunisolarkalender im Beispiel aus? Nehmen wir den ersten Kalender, welcher 235 Monate für 19 Jahre rechnet. Wie wir schon weiter oben wissen, können 228 Monate davon auf 19 Jahre gleichmäßig verteilt werden. Das wären dann 12 Monate für jedes Jahr. 7 Monate bleiben übrig, also müsste je 19-Jahr-Epoche 7 Jahre dabei sein, die 13 Monate statt der 12 Monate aufweisen.
Der jüdische oder hebräische Kalender, der übrigens so ein Lunisolarkalender ist, teilt die 7 Extramonate zu den Jahren 3, 6, 8, 11, 14, 17 und 19 zu. Bei den Monaten gibt es ähnliche Regeln wie bei den Mondkalendern. Im jüdischen Kalender beginnt ein Tag mit dem Sonnenuntergang. Sobald an einem Ort die Sonne untergegangen ist, ist der Tag vorbei und ein neuer fängt an. Deshalb gibt es auch keine wirklichen Zeitzonen für den jüdischen Kalender. Die Monate beginnen mit der Sichtung des Neumonds, aber im jüdischen Kalender ist davon nicht das ganze System abhängig, wie im islamischen Kalender. Dieses Jahr zum Beispiel beginnen die meisten jüdischen Monate einen Tag nach Neumond, an 3 Monaten gleich zum Neumond, an einem Monat erst zwei Tage nach Neumond. Das jüdische Modell weicht vom reinen Sonnenkalender um etwa ± 2 Wochen. Um mit dem Mond synchron zu sein, wechseln sich die hohlen und die vollen Monaten mit jeweils 29 und 30 Tagen ab. Weil ein Monat bisschen mehr als 29,5 Tage lang andauert, bekommen 4 der 12 gewöhnlichen Jahre im Monat Marcheschwan, das ist der zweite Monat des jüdischen Jahrs, welcher zwischen Anfang Oktober und Anfang November für unsere Zeitrechnung steht, einen Tag mehr als sonst.
Die ganzen Regeln dahinter sind nochmal komplizierter, beim dritten Monat namens Kislew wird auch manchmal einen Tag abgezogen. Der Grund liegt im Grunde dabei, dass das jüdische Neujahrsfest Rosch ha-Schana nicht an manchen Wochentagen stattfinden kann.
Tatsächlich ist unser gregorianische Kalender gar nicht so unähnlich zu einem Lunisolarkalender. Allerdings ist der gregorianische Kalender definitiv ein Sonnenkalender, da die Monate, die wir zählen, sind in Wahrheit nur Abschnitte eines Jahres. Man kann in unserem Kalender nicht sagen, dass wir immer am Monatsersten jetzt Neumond haben. 12 gleich große Monate ergeben ein Jahr, also gibt es 30 Tage im Monat, aber einige Monate müssen 31 Tage haben.
Die Zeitzonen
Allerdings kamen auch hier Probleme auf, und zwar erst im 18ten Jahrhundert. Da die Erde kugelförmig ist, mehr oder weniger, kann zum Beispiel nur auf einer Hälfte der Erde Nacht sein und auf der anderen Hälfte Tag. Auch ist die Zeit bis zum Mittag, oder Sonnenuntergang unterschiedlich lang, sodass man hier nur noch 6 Stunden zum Sonnenuntergang hat, und 400 Kilometer weiter allerdings noch 7 Stunden. Das ist nur ein Beispiel und muss auch nicht so in Realität passieren. Was aber in der Realität passierte, dass jeder Ort besonders in Mitteleuropa seine eigene gültige Zeit hat. Das heißt Angelegenheiten innerhalb der Stadt und seinem Umfeld sind kein Problem, aber wenn du per Eisenbahn oder Postkutsche deine Freundin oder deinen Freund in der Stadt 100 Kilometer weiter treffen willst, sind die Uhrzeiten dort vor Ort um einige Minuten unterschiedlich. Das kann bereits zu Verwirrung führen. Ich komme um diese Uhrzeit an, allerdings dauert die Fahrt in Wahrheit länger oder kürzer, als man es denken würde. Oder die Ankunftszeit ist in Wahrheit anders.
Um diese Verwirrung zu umgehen, hat man dann auch die Zeitzonen aufgeteilt. Es gibt 24 Stunden an einem Tag, und im idealen Fall würden sie auf 360° / 24 Std = 15 Grad zu je einer Stunde aufgeteilt werden. In der Realität sind besonders die Landmassen wegen verschiedener nationaler Interessen verschiedene Zeitzonen verwendet, obwohl die eigentliche Ortszeit schon um mehr als eine halbe Stunde schon anders wäre. In Europa haben zum Beispiel die meisten Länder UTC+1 als Zeitzone, plus Sommerzeit (engl.: daylight saving time). Noch krasser ist China: Auf der ganzen Staatsfläche gibt es nur eine Zeitzone, und zwar UTC+8, obwohl China flächenmäßig das drittgrößte Land der Welt ist und eine Längsausdehnung von 61,27 Grad hat.

Die Einheiten
Wichtige Einheiten hier, der dicke Strich separiert die 7 Elementareinheiten von den anderen:
| Wichtige Einheiten in der Astronomie | ||||
| Name | Dimension | Symbol | Definition | Erklärung |
| Sekunde | Zeit | s | ΔvCs = 9 192 631 770 Hz (s-1) | Die Frequenz der Strahlung, die bei dem Übergang zwischen den beiden Hyperfeinstrukturniveaus des Isotops 133Cs abgestrahlt wird, ist fest definiert, von der 9192631770fachen Periodendauer kommt dann die Sekunde her. |
| Meter | Länge | m | 1 m = 299 792 458-1 c s | Der Meter ist an die Lichtgeschwindigkeit gebunden; es ist die Strecke, die das Licht im Vakuum im Zeitraum von dem 299792458ten Teil einer Sekunde zurücklegt. |
| Kilogramm | Masse | kg | ℎ = 6,626 070 15 × 10-34 Js (kg m2 s-1) | Das Kilogramm ist heutzutage als Folge des Planckschen Wirkungsquantum definiert. Dieses ist wiederum eine fundamentale Konstante, die Energie mit der Frequenz verbindet (oder Impuls mit der Länge) |
| Ampere | Stromstärke | A | 1 A = C s-1 = W V-1 | Die Elementarladung ist die Konstante hinter dem Ampere. Coulomb (das C) und Ampere verhalten sich ähnlich wie Watt und Joule: Ampere ist die Stromstärke, wieviel Ladung an einem Querschnitt z.B. in einer Sekunde vorbeirauscht. |
| Kelvin | Temperatur | K | kB = 1,380 649 × 10-23 J K-1 | Anhand der Boltzmann-Konstante ist die Einheit Kelvin definiert, sie beginnt beim absoluten Nullpunkt (-273,15 °C) und hat dieselbe Skala wie Grad Celsius. |
| Mol | Stoffmenge | mol | 1 mol = 6,022 140 76 × 1023 Teilchen | Diese Anzahl an Atomen…Molekülen…andere Teilchen ergibt ein Mol. Siehe Avogadro-Konstante. |
| Candela | Lichtstärke | cd | 1 cd = lm sr-1 | Die Lichtmenge, die in einen bestimmten Raumwinkel abgegeben wird. |
| Newton | Druck, Kraft | N | 1 N = kg m s-2 | Z.B Ein Objekt mit 102 g Masse (etwa wie Tafel Schokolade) erzielt bei der Erdanziehungskraft von ca. 9,806 m/s2 eine Kraft von einem Newton. |
| Joule | Energie | J | 1 kg m2 s-2 = N m = C V = W s = Pa m3 | Die Energie, die genutzt wird, wenn für einen Prozess eine Leistung von einem Watt für eine Sekunde benötigt wird, die Ladung von einem Coulomb /kuˈlõː/ durch ein elektrisches Potenzial von einem Volt bewegt wird, bzw. wenn ein Strom von einem Ampere mit einer Spannung von einem Volt für eine Sekunde gehalten wird, ein Objekt mit 2 Kilogramm Masse zu 1 m/s zu beschleunigen, ein Gramm Wasser, um etwa 0,239 Kelvin zu erwärmen, 10 Millionen Erg sind ein Joule. |
| Watt | Leistung | W | 1 J s-1 = V A = kg m2 s-3 = N m s-1 | Die Energiekapazität sozusagen, in Energieverbraucher oder Energieerzeuger hat eine bestimmte Kapazität und je mehr Zeit vergeht, desto mehr Energie wurde auch verbraucht oder erzeugt, ein Mensch, der ein Kind mit 30 kg 3 Meter 5 Sekunden lang eine Leiter hochtragt und gegen die Erdschwerkraft ankämpft, erbringt eine Leistung von ca. 175 Watt ohne die Leistung die eigenen Körperteile zu bewegen. |
| Erg | Energie | erg | 1 g cm2 s-2 | 10-7 J = 1 Erg |
| Astronomische Einheit | Länge | AE | 1 AE = 149 597 870 700 m | Die große Halbachse / mittlere Distanz zwischen der Erde und der Sonne |
| Lichtjahr | Länge | lj, ly | 1 lj = 9 460 730 472 580 800 m | Die Strecke, die Licht in einem Jahr zurücklegen kann, wenn die Lichtgeschwindigkeit 299 792 458 m/s beträgt, und es 31 557 600 Sekunden in einem julianischen Jahr (365,25 d) gibt. |
| Lichtsekunde | Länge | -(unüb.) | 1 c s = 299 792 458 m | Die Strecke, die Licht in einer Sekunde zurücklegen kann |
| Monddistanz / Lunar Distance | Länge | ld | 1 ld = 383 397,791 6 km zur Epoche J2000.0 | Die mittlere Entfernung Erde – Mond |
| Bogengrad | Ebener Winkel | ° | 1/360 eines Vollkreises | Etwa die scheinbare Größe des Daumens bei ausgestreckter Hand |
| Bogensekunde | Ebener Winkel | ″ | 1/3600 eines Bogengrades, 1/1296000 eines Vollkreises | Etwa die scheinbare Größe eines Daumens in zwei Kilometer Entfernung, oder die eines Dorfes auf der Erde vom Mond aus gesehen |
| Parsec | Länge | pc | 1 pc = 648 000 AE π-1 | Die Annäherung der Größe einer Parallaxe von einer Bogensekunde bei einer Basislinie von einer Astronomischen Einheit |
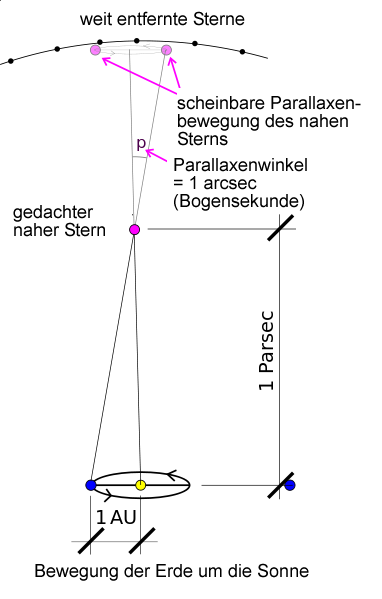
Stellarparallax_parsec1_de.png
Interessant zu erwähnen ist, dass das Erg aus dem CGS-System kommt (Zentimeter-Gramm-Sekunde) und immer noch einigermaßen oft in der Astronomie gebraucht wird, und die astronomische Einheit nicht wirklich metrisch ist, aber dennoch gerne in den Populärwissenschaften erwähnt wird.
Die Zeit und der Raum
Die Zeit ist relativ. Ein kurzer Einblick hier, was das bedeutet.
Dieses Thema streife ich hier nur kurz an, da ich es noch ausführlicher in einigen Monaten im passenden Teil der Geschichte der Astronomie behandeln werde, und möglicherweise auch noch zu anderen Gegebenheiten.
Nach dem die Michelson-Morley-Experimenten, die herausfinden wollten, ob es ein Medium für das Licht gibt, welches man zu der Zeit sich hauptsächlich als eine Welle vorstellte. Eine Welle ist klassischerweise eine sich ausbreitende Druckveränderung im Medium, welche im Prinzip von einer Sinuskurve ausgeht, welche also eine Amplitude, Wellenlänge und so weiter hat, so wie zum Beispiel Schall. Dieses Lichtmedium nannte man den Äther. Die Experimente dessen Aufbauten erinnern an die Aufbauten für Gravitationswellenobservatorien; es gibt zwei Arme, die im rechten Winkel zueinander stehen und wenn es einen Äther gibt und die Erde um die Sonne kreist, müsste sich die Geschwindigkeit des Lichts sich im Laufe des Jahres verändern, wenn der Äther alles durchdringt und wir uns in Bewegung befinden.
Das Experiment ging nicht auf, es wurde wohl keine signifikante Veränderung gezeigt, den Äther gab es zumindest nicht in der Form.
Irgendwann kam dann, wer hätte es gedacht, der Herr Einstein und hat seine Theorien aufgestellt, welcher als Hintergrundinformation schon von Licht interessiert war. Damals war Licht auch noch nicht wirklich erforscht und Herr Einstein hat dazu durchaus auch beigetragen, wofür er auch seinen Nobelpreis 1921 (erhalten erst 1922) bekommen hat.
Herr Einstein formulierte tatsächlich zwei Theorien, die spezielle Relativitätstheorie 1905 und die allgemeine Relativitätstheorie 1914/15. Die spezielle Relativitätstheorie bespricht die Relativität der Zeit, Gleichzeitigkeit und der Länge (und damit des Raumes). Die allgemeine Relativitätstheorie behandelt die relativistischen Effekte, die der Raum und die Zeit als Raumzeit haben, auch ohne die Bedingung, dass die beiden Systeme, die aneinander verglichen werden, statische Bewegungen innehaben. So wird im Vorfeld Gravitation und gewöhnliche Beschleunigung gleichgesetzt, was zur Auswirkung die Folge hat, dass eine Masse, die Gravitation erzeugt, die Raumzeit ebenso krümmt wie zwei Inertialsysteme hoher statischer relativer Geschwindigkeiten. Jedoch ist die ART viel umfangreicher als die SRT und damit Thema eines zukünftigen Beitrags.
Einstein kommt somit zum Schluss, dass Zeit und Raum eigentlich nicht getrennt zu betrachten sind, weil sie besonders nach der SRT nur zusammen den ein und denselben Effekt im Grunde haben. Und das kann man auch schön und knapp demonstrieren:
Die Myonen, die Sekundärteilchen in der kosmischen Strahlung sind, entstehen rund 10 Kilometer über dem Erdboden im Durchschnitt. Deren Halbwertszeit beträgt etwa 1 522,8 ns (Nanosekunden), deren typische Geschwindigkeit in Richtung Erde beträgt 0,995 c (das 0,995fache der Lichtgeschwindigkeit c). Ein durchschnittliches Myon kann also 0,995 c × 1 522,8 ns ≈ 454 ¼ m in die Erdatmosphäre ab 10 km Höhe eintauchen. Mit der Geschwindigkeit 0,995 c bräuchte man 33,356 409 519 8 µs (Mikrosekunden) für 10 Kilometer. In dieser Zeit sind allerdings schon 33,356 409 519 8 µs / 1,522 8 µs = 21,904 655 581 7 Halbwertszeiten eines Myons vergangen. Demnach sollten nur 0,000 025 470 743 667 8 % aller Myonen auf der Erdoberfläche ankommen. Dennoch kommen auf Meereshöhe 100 kosmische Myonen je Quadratmeter und Sekunde zusammen. An dieser Stelle rechne ich nicht weiter, da die Prüfung, ob das Niveau auf 10 km Höhe in der Atmosphäre zu dem hier unten passt, komplizierter als ein Unterthema eines eh schon großen Beitrags wäre. Ich habe jetzt die Myonen berechnet, die direkt senkrecht zu Erde kommen, und nicht in einem schrägen Winkel zum Beobachter, das Ergebnis, wieviele Myonen auf einen Punkt der Erde landen, sollte also um einen Prozentsatz größer sein. Außerdem sehen wir auch schon so, dass die 100 Myonen und die 0,000 03 und so weiter Prozent vermutlich kaum zusammenpassen. Es wäre ja sonst so, dass in 10 km Höhe fast 400 Millionen Myonen sich bilden müssten. Da fehlt also was.
0,995 c ist sehr nah an der Lichtgeschwindigkeit, und wenn ein massebehaftetes Objekt mit keiner Energie exakt die Lichtgeschwindigkeit treffen kann, können massebehaftete Objekte die Geschwindigkeit ganz gut annähern. Man rechnet grob ab Geschwindigkeiten von 0,1 c bis 0,2 c mit relativistischen Effekten, wobei sie auch schon vorher zum Teil erhebliche Auswirkungen haben kann, wie z.B. der relativistische Anteil der Apsidendrehung.
Ein nicht minder genialer Physiker namens Hendrik Antoon Lorenz ist schon vorher auf die nach ihm benannte Lorenzkontraktion gestoßen, jedoch unter falscher Annahme. Erst Einstein kam im Rahmen seiner SRT auf die Lorenzkontraktion erneut, benutzte diese Formel aber für die Zeitdilatation. Es gibt die Zeitdilatation und die Längenkontraktion, die dafür sorgen, dass die Raumzeit zwar miteinanderhängt, aber auch, dass Licht allen Inertialsystemen hinweg (das ist ein System, welche keine oder zumindest eine marginale Beschleunigung als Ganzes erfährt, wie z.B. die ganze Erde oder ein Raumschiff) die gleiche Geschwindigkeit im Vakuum erreichen kann. Das Ergebnis der Lorenzkontraktion ist der Gamma-Faktor, welcher allein von der Geschwindigkeit relativ zum Beobachter abhängig ist. Es ist ein Faktor, der mit der Zeit, die am Beobachter vergangen ist, multipliziert wird. Und so sieht die Lorenzkontraktion aus: γ = 1 / √(1 – (v2/c2)), oder bisschen einladender in diesem bescheidenem Formelformat: γ = 1 / (1 – (v2/c2))1/2 . Wenn wir unsere Werte einsetzen: γ = 1 / (1 – 0,9952)1/2 ≈ 10,0125. Dieser Wert bedeutet, dass wenn das Myon eine Uhr bei seinem Flug in die Erdatmosphäre hätte und es mit einer Uhr vom Beobachter vergleichen würde, die Uhr des Myons um etwa den Faktor 10,0125 langsamer geht als die vom Beobachter und andersherum 10,0125-mal schneller. Großartig! Also hat ein Myon in Wahrheit eine Halbwertszeit von dem Gamma-Faktor mal der herkömmlichen Halbwertszeit, was zusammengerechnet 15 247 Nanosekunden ergibt, die die Myonen nun vom Stand des Beobachters haben. In dieser Zeit schafft das durchschnittliche Myon etwa 4 548,1 Meter.
Ein Effekt ist aber noch nicht berücksichtigt, nämlich die Längenkontraktion. Während der Effekt um die Veränderung oder die Stauchung/Streckung der Zeit durch die Lichtuhr relativ einfach erklärbar ist, weil sich ja das Myon bewegt, relativ zur stehenden Erde. Andererseits könnte genauso gut ein Beobachter auf diesem Myon sagen, dass sich die Erde auf das Myon zu bewegt, das ja beide Inertialsysteme immer noch gleichwertig sind. Für diesen Beobachter auf dem Myon sieht es aber auch so aus, als ob die Strecke sich um den Gammawert gestaucht hat, allerdings nimmt er die Zeit normal auf dem Myon wahr, denn es gibt ja auch kein Grund, warum für den Beobachter auf dem Myon die Zeit anders vergeht, weil für den Myonen-Beobachter bewegt sich das Myon ja auch selbst nicht. Dann müsste ja auch die Halbwertszeit anders als normal sein. Hier ist die Strecke von 10 km plötzlich auf ca. 987,7 Meter zusammengeschrumpft.
An dieser Stelle möchte ich die Verwirrung etwas lösen, denn in unserem Alltag sind für die meisten Handlungen relativistische Effekte irrelevant, da ein Kilometer ein Kilometer bleibt, und eine Sekunde eine Sekunde. Handelt sich aber stattdessen um Geschwindigkeiten, die mehrere Tausend Meter pro Sekunde, zum Beispiel, überschreiten, dann sollte man relativistische Effekte berücksichtigen.
Es gibt immer zwei Systeme: (keine Ahnung, ob diese Systeme echte Namen haben, ich habe sie hier jetzt mal einfach so genannt, im Zweifelsfall lieber nicht nutzen) das bewegte System und das Vergleichssystem. Das bewegte System bewegt sich relativ zum Vergleichssystem, wobei auch ein Beobachter im bewegten System weiß, dass er sich bewegt, weil das Vergleichssystem entweder viel größer ist, oder sich gar nicht bewegen kann, weil es dazu keine Technik hätte.
Innerhalb jedes Inertialsystems gelten die Naturgesetze ausnahmslos, daher ist in diesen Systemen jeweils eine Sekunde eine Sekunde und eine Kilometer ein Kilometer. Da wir aber aufgrund der Lichtuhr (siehe Grafik) aus der Ansicht des Vergleichssystems in das bewegte System wissen, dass vergleichsweise weniger Zeit im bewegten System vergeht, haben wir verschiedene Zeiten auf einmal, wenn man beide Uhren vergleichen würde. Aus dem Myonen-Beispiel von oben vergehen laut der Lorentzkontraktion 10,0125 Sekunden im bewegten System, während im Vergleichssystem (die Erde) nur eine Sekunde vergeht. Innerhalb des bewegten Systems vergeht aber, wie schon gesagt, deswegen die Zeit nicht anders, weswegen wir eine Erklärung brauchen, warum wir im bewegten System 10,0125-mal schneller an allem vorbeifliegen, da wir ja im Vergleich zum Vergleichssystem uns trotzdem 10,0125-mal schneller agieren können. Und die Erklärung ist quasi der relativistische Effekt nochmal, aber komplementär. Das bewegte System reist auf sein Ziel zu. Aber da das bewegte System ein gleichwertiges Inertialsystem ist, kann man auch genauso gut sagen, dass das Ziel auf das bewegte System zufliegt. Es ist eben nur eine Interpretationssache. Um es aufzulösen, verkleinert sich die Reiselänge um denselben Faktor von 10,0125, um den relativistischen Effekt komplementär wieder ins Reine zu bringen, da es im Grunde die einzige Lösung zum Fakt ist, dass sich das bewegte System 10,0125 schneller bewegen müsste.
Ich fürchte, dass das nicht viel einfacher nun war, vielleicht hat es aber geholfen. Ich empfehle auch gerne selbst im Taschenrechner das nachzurechnen. Ich packe noch eine Grafik dazu.
Hier mal eine gleiche Rechnung für die kinetische Energie am Rande: Ein Myon, welches mit 0,995 c fliegt, hat nach Ekin = m0 × c2 (1 / (1 – v2/c2)0,5 – 1) = 1,883 531 627 × 10–28 kg × (299 792 458)2 m/s × (1 / (1 – 0,9952)0,5 – 1) ≈ 1,525 670 441 8 × 10–10 J ≈ 952 248 591 eV etwas mehr als 950 MeV kinetische Energie, ohne den relativistischen Effekt, würde es eine kinetische Energie von nur ca. 52,3 MeV aufweisen.
Was also ist die sphärische Astronomie?
Zum Abschluss können wir nun zusammenfassen, dass die sphärische Astronomie die benutzten Systeme aus der Astronomie thematisiert. Das sind die Systeme, die die Bedingungen der astronomischen Forschung vorgeben und uns aber auch von Nutzen sein sollen, um die Welt außerhalb der Erde systematisch und wissenschaftlich zu beschreiben und zu erkunden. Das ist zum Beispiel das Koordinatensystem, die z.B. die Ekliptik beinhaltet und man nicht nur für einfache Positionsangaben benutzen kann, sondern auch, dass man weiß, wo man überall auf der Erde den und den Stern zu welcher Uhrzeit und Datum sehen kann. Aber auch, um zu wissen, wie die Einheiten zusammen funktionieren, und was uns das in der Astronomie bringt. Aus diesem Grund ist es auch der Bereich der Astronomie, welcher am ehesten sich nicht verändert, da alles schon festgemacht ist.
Zu diesem Beitrag wird es ein Folgebeitrag geben – vermutlich noch dieses Jahr, es sei denn, es zieht sich weiterhin alles in die Länge 🙂
Quellen:
- https://en.wikipedia.org/wiki/Absolute_magnitude
- https://de.wikipedia.org/wiki/Absolute_Helligkeit, bzw. https://physik.cosmos-indirekt.de/Physik-Schule/Absolute_Helligkeithttps://de.wikipedia.org/wiki/Julianisches_Datum
- https://astronomy.stackexchange.com/questions/18391/why-is-jd-2451545-0-january-1-2000-noon-instead-of-jd-2451558-0
- https://en.wikipedia.org/wiki/Rotation_period
- https://de.wikipedia.org/wiki/Jahr#In_der_Astronomie
- https://en.wikipedia.org/wiki/Year
- https://en.wikipedia.org/wiki/Sidereal_year
- https://en.wikipedia.org/wiki/Lunar_month
- https://de.wikipedia.org/wiki/Mondbahn
- https://de.wikipedia.org/wiki/Lunation
- https://de.wikipedia.org/wiki/Islamischer_Kalender
- https://en.wikipedia.org/wiki/Islamic_calendar
- https://de.wikipedia.org/wiki/Lunisolarkalender
- https://de.wikipedia.org/wiki/J%C3%BCdischer_Kalender
- https://en.wikipedia.org/wiki/Hebrew_calendar
- https://de.wikipedia.org/wiki/Zeitzone
- https://en.wikipedia.org/wiki/Time_zone
- https://en.wikipedia.org/wiki/International_System_of_Units
- https://de.wikipedia.org/wiki/Internationales_Einheitensystem
- https://de.wikipedia.org/wiki/Erg_(Einheit)
- https://de.wikipedia.org/wiki/Parsec
- https://de.wikipedia.org/wiki/Spezielle_Relativit%C3%A4tstheorie
- Das Kompendium der Astronomie, Hans-Ulrich Keller, 2019, Kosmos, ISBN 978-3-440-16276-7
