Die Geschichte der Astronomie, Teil 26

Tycho und Kepler, Teil 7: Keplers Gesetze

Kepler nutzte Tychos Beobachtungsdaten sehr, um seine wirklich bekannten klassischen Gesetze der Bewegung aufstellen zu können. Als Basis für seine Theorie studierte er insbesondere die Marsstellungen, die Tycho Brahe aufgezeichnet hat. Mit den Marsstellungen hoffte er auf Erfolg – und dieser blieb nicht aus!

Kepler vermutete hinter den Bewegungen des Mars eine Ellipse um die Sonne, eine Ellipse ist auch ein schräger Kegelschnitt. Kepler kannte nämlich genau die Eigenschaften von Kegelschnitten, er hatte Apollonius von Perges Werk genau studiert.
Es erscheint mir wirklich bizarr, denn zu Perges Werk hatte Ptolemäus und Kopernikus theoretisch Zugang, aber beide nahmen wahrscheinlich unabhängig von einander an, dass die Planeten Kreisbahnen beschreiben. Jedoch war es für diese Zeit, vermutlich genau aus dem Grund, dass die Gelehrten die Werke von beiden kennen, noch absurd, so wie sein älteres Werk über die fünf platonischen Körper, es erschien den damaligen Gelehrten absolut unverständlich, weswegen denn die Planeten eine elliptische Bahn um die Sonne folgen sollen. Was sollen denn diese Ellipsen überhaut mit dem System der Welt gemeinsam haben?
Doch auch wenn es noch einige Zeit vergehen musste, bis Keplers Gesetze Anerkennung finden, entsprechen sie dem aktuellen Verständnis der Physik.

1. Gesetz: Die Planeten bewegen sich auf Ellipsen, in deren einem Brennpunkt die Sonne steht.
   Eine Ellipse oder ein Kegelschnitt besitzt zwei symmetrisch zueinanderstehende Brennpunkte auf der Längsachse. Brennpunkt deswegen, weil wenn ein Lichtstrahl auf die Begrenzung des Kegelschnitts oder der Ellipse trifft, wird er zu einem der Brennpunkte reflektiert werden.
2. Gesetz: Der Radiusvektor (allgemeiner bekannt als Fahrstrahl) von der Sonne zum Planeten überstreicht in gleichen Zeiten gleichen Flächen.
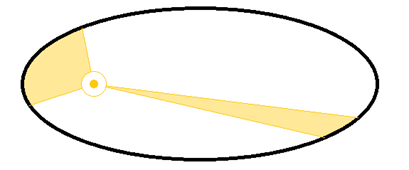
   Das bedeutet, dass wenn ein uns ausgedachter Planet auf einer ausgedachten exzentrischen Flugbahn gerade der Sonne fern ist, so ist der Planet zwar langsamer, aber die Fläche wird durch den größeren Abstand genauso groß sein, wie wenn ein Planet zwar sehr viel von seiner Strecke zurückgelegt hat, aber durch den kleineren Abstand zur Sonne dann doch nur die gleiche Fläche geschafft hat. Wegen dem Verständnis eine eigens dafür erstellte Grafik.
3. Gesetz: Die Quadrate der Umlaufzeiten der Planeten verhalten sich wie die Kuben der großen Halbachsen ihrer Bahnellipsen. U² = a³
   Der Quotient gilt auch sonst für alle Himmelskörper, die sich in einer Umlaufbahn befinden. Ein Rechenbeispiel: U² = a³ . Also gilt für U folgendes: U = sqrt(a³) = a × sqrt(a), und für a folgendes: a = 3yrt(U²). Dabei sind AE und Jahre gleichgestellt.
   Da die Formeln aus Word nicht funktionieren, hier nochmal als Bild:

Seine ersten beiden Gesetze beschreiben die Stellungen der Planeten und man könnte die Planetenpositionen ziemlich exakt damit berechnen, wenn man die genauen Stellungen der Planeten kennt. Wenn sie natürlich zu ungenau sind, verfälscht man sich das Ergebnis damit selbst. Erstmals konnte jemand die Bahnbewegung der Planeten richtig erklären und berechnen. Von seinem dritten Gesetz war er selbst beeindruckt. Er vermutete trotzdem ähnlich wie Kopernikus und Ptolemäus, dass der Quotient der Umlaufzeit und der großen Halbachse in einem göttlichen Verhältnis stehen muss, denn er konnte unmöglich für alle Planeten zufällig der gleiche sein.

Sein Vermächtnis sind die Rudolfinischen Tafeln und seiner drei Gesetze, die er mit Verzögerung veröffentlichen konnte. Zu der Zeit tobte nämlich der Dreißigjährige Krieg und viele feindliche Bilder der katholischen, oder sogar der Protestanten, wurden zu dieser Zeit leicht eliminiert. Seine mathematischen Fähigkeiten und Erkenntnissen zu den Kegelschnitten und Tycho Brahes äußerst akkuraten Messungen lieferten ein noch ungenutztes großes Potenzial. 1628 konnte er seine Theorie der gelehrten Welt zugänglich machen. Da sich wissenschaftliche Erkenntnisse jedoch immer noch sehr langsam verbreiten konnten, waren die jungen Astronomen Jeremiah Horrocks und William Crabtee vermutlich im Jahr 1639 die Ersten, die die Rudolfinischen Tafeln benutzten – und das immerhin nach 10 Jahren (und wenigen Monaten). Trotzdem erlangte seiner Zeit keiner von Keplers Werke so großes Aufsehen, wie die von Kopernikus zu seiner Zeit, oder eine Generation nach ihm, die Werke von Galileo Galilei.